Chapter 17
More of a Good Thing: Multiple Regression
IN THIS CHAPTER
 Understanding what multiple regression is
Understanding what multiple regression is
 Preparing your data and interpreting the output
Preparing your data and interpreting the output
 Understanding how interactions and collinearity affect regression analysis
Understanding how interactions and collinearity affect regression analysis
 Estimating the number of participants you need for a multiple regression analysis
Estimating the number of participants you need for a multiple regression analysis
Chapter 15 introduces the general concepts of correlation and regression, two related techniques for detecting and characterizing the relationship between two or more variables. Chapter 16 describes the simplest kind of regression — fitting a straight line to a set of data consisting of one independent variable (the predictor) and one dependent variable (the outcome). The formula relating the predictor to the outcome, known as the model, is of the form 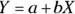 , where Y is the outcome, X is the predictor, and a and b are parameters (also called regression coefficients). This kind of regression is usually the only one you encounter in an introductory statistics course, because it is a relatively simple way to do a regression. It’s good for beginners to learn!
, where Y is the outcome, X is the predictor, and a and b are parameters (also called regression coefficients). This kind of regression is usually the only one you encounter in an introductory statistics course, because it is a relatively simple way to do a regression. It’s good for beginners to learn!
This chapter extends simple straight-line regression to more than one predictor — to what’s called the ordinary multiple linear regression model, or more simply, multiple regression.
Understanding the Basics of Multiple Regression
In Chapter 16, we outline the derivation of the formulas for determining the parameters of a straight line so that the line — defined by an intercept at the Y axis and a slope — comes as close as possible to all the data points (imagine a scatter plot). The term as close as possible is operationalized as a least-squares line, meaning we are looking for the line where the sum of the squares (SSQ) of vertical distances of each point from to the line is the smallest. SSQ for a fitted line is smallest for the least-squares line than for any other line you could possibly draw.
The same idea can be extended to multiple regression models containing more than one predictor (which estimates more than two parameters). For two predictor variables, you’re fitting a plane, which is a flat sheet. Imagine fitting a set of points to this plane in three dimensions (meaning you’d be adding a Z axis to your X and Y). Now, extend your imagination. For more than two predictors, in regression, you’re fitting a hyperplane to points in four-or-more-dimensional space. Hyperplanes in multidimensional space may sound mind-blowing, but luckily for us, the actual formulas are simple algebraic extensions of the straight-line formulas.
In the following sections, we define some basic terms related to multiple regression, and explain when you should use it.
Defining a few important terms
- Ordinary: The outcome variable is a continuous numerical variable whose random fluctuations are normally distributed (see Chapter 24 for more about normal distributions).
- Multiple: The model has more than two predictor variables.
- Linear: Each predictor variable is multiplied by a parameter, and these products are added together to estimate the predicted value of the outcome variable. You can also have one more parameter thrown in that isn’t multiplied by anything — it’s called the constant term or the Intercept. The following are examples of linear functions used in regression:
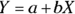 (This is the straight-line model from Chapter 16, where X is the predictor variable, Y is the outcome, and a and b are parameters.)
(This is the straight-line model from Chapter 16, where X is the predictor variable, Y is the outcome, and a and b are parameters.)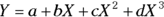 (In this multiple regression model, variables can be squared or cubed. But as long as they’re multiplied by a coefficient — which is a slope from the model — and the products are added together, the function is still considered linear in the parameters.)
(In this multiple regression model, variables can be squared or cubed. But as long as they’re multiplied by a coefficient — which is a slope from the model — and the products are added together, the function is still considered linear in the parameters.)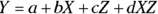 (This multiple regression model is special because of the XZ term, which can be written as
(This multiple regression model is special because of the XZ term, which can be written as  , and is called an interaction. It is where you multiple two predictors together to create a new interaction term in the model.)
, and is called an interaction. It is where you multiple two predictors together to create a new interaction term in the model.)
- A collection of predictor variables may be designated by a subscripted variable and the corresponding coefficients by another subscripted variable, like this:
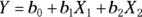 .
. - In practical research work, the variables are often given meaningful names, like Age, Gender, Height, Weight, Glucose, and so on.
- Linear models may be represented in a shorthand notation that shows only the variables, and not the parameters, like this: Y = X + Z + X * Z instead of Y = a + bX + cZ + dX * Z or Y = 0 + X + Z + X * Z to specify that the model has no intercept. And sometimes you’ll see a “~” instead of the “=”. If you do, read the “~” as “is a function of,” or “is predicted by.”
Being aware of how the calculations work
Fitting a linear multiple regression model essentially involves creating a set of simultaneous equations, one for each parameter in the model. The equations involve the parameters from the model and the sums of various products of the dependent and independent variables. This is also true of the simultaneous equations for the straight-line regression in Chapter 16, which involve estimating the slope and intercept of the straight line and the sums of 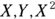 , and XY. Your statistical software solves these simultaneous equations to obtain the parameter values, just as is done in straight-line regression, except now, there are more equations to solve. In multiple as in straight-line regression, you can also get the information you need to estimate the standard errors (SEs) of the parameters.
, and XY. Your statistical software solves these simultaneous equations to obtain the parameter values, just as is done in straight-line regression, except now, there are more equations to solve. In multiple as in straight-line regression, you can also get the information you need to estimate the standard errors (SEs) of the parameters.
Executing a Multiple Regression Analysis in Software
Before executing your multiple regression analysis, you may need to do some prep work on the variables you intend to include in your model. In the following sections, we explain how to handle the categorical variables you plan to include. We show you how to examine these variables through making several charts before you run your analysis. If you need guidance on what variables to consider for your models, read Chapter 20.
Preparing categorical variables
The predictors in a multiple regression model can be either numerical or categorical (Chapter 8 discusses the different types of data). In a categorical variable, each category is called a level. If a variable, like Setting, can have only two levels, like Inpatient or Outpatient, then it’s called a dichotomous or a binary categorical variable. If it can have more than two levels, it is called a multilevel variable.
Figuring out the best way to introduce categorical predictors into a multiple regression model is always challenging. You have to set up your data the right way, or you’ll get results that are either wrong, or difficult to interpret properly. Following are two important factors to consider.
Having enough participants in each level of each categorical variable
Before using a categorical variable in a multiple regression model, you should tabulate how many participants (or rows) are included in each level. If you have any sparse levels — row frequencies in the single digits — you will want to consider collapsing them into others. Usually, the more evenly distributed the number of rows are across all the levels, and the fewer levels there are, the more precise and reliable the results. If a level doesn’t contain enough rows, the program may ignore that level, halt with a warning message, produce incorrect results, or crash. Worse, if it produces results, they will be impossible to interpret.
Imagine that you create a one-way frequency table of a Primary Diagnosis variable from a sample of study participant data. Your results are: Hypertension: 73, Diabetes: 35, Cancer: 1, and Other: 10. To deal with the sparse Cancer variable, you may want to create another variable in which Cancer is collapsed together with Other (which would then have 11 rows). Another approach is to create a binary variable with yes/no levels, such as: Hypertension: 73 and No Hypertension: 46. But binary variables don’t take into account the other levels. You could also make a binary Diabetes variable, where 35 were coded as yes and the rest were no, and so on for Cancer and Other.
Similarly, if your model has two categorical variables with an interaction term (like Setting + Primary Diagnosis + Setting * Primary Diagnosis), you should prepare a two-way cross-tabulation of the two variables first (in our example, Setting by Primary Diagnosis). You will observe that you are limited by having to ensure that you have enough rows in each cell of the table to run your analysis. See Chapter 12 for details about cross-tabulations.
Choosing the reference level wisely
For each categorical variable in a multiple regression model, the program considers one of the categories to be the reference level and evaluates how each of the other levels affects the outcome, relative to that reference level. Statistical software lets you specify the reference level for a categorical variable, but you can also let the software choose it for you. The problem is that the software uses some arbitrary algorithm to make that choice (such as whatever level sorts alphabetically as first), and usually chooses one you don’t want. Therefore, it is better if you instruct the software on the reference level to use for all categorical variables. For specific advice on choosing an appropriate reference level, read the next section, “Recoding categorical variables as numerical.”
Recoding categorical variables as numerical
Data may be stored as character variables — meaning the variable for primary diagnosis (PrimaryDx) may be contain character data, such as Hypertension, Diabetes, Cancer, and Other. Because it is difficult for statistical programs to work with character data, these variables are usually recoded with a numerical code before being used in a regression. This means a new variable is created, and is coded as 1 for hypertension, 2 for diabetes, 3 for cancer, and so on.
For categorical variables with more than two levels, it’s more complicated. Even if you recode the categorical variable from containing characters to a numeric code, this code cannot be used in regression unless we want to model the category as an ordinal variable. Imagine a variable coded as 1 = graduated high school, 2 = graduated college, and 3 = obtained post-graduate degree. If this variable was entered as a predictor in regression, it assumes equal steps going from code 1 to code 2, and from code 2 to code 3. Anyone who has applied to college or gone to graduate school knows these steps are not equal! To solve this problem, you could select one level for the reference group (let’s choose 3), and then create two binary indicator variables for the other two levels — meaning one for 1 = graduated high school and 2 = graduated college. Here’s another example of coding multilevel categorical variables as a set of indicator variables, where each level is assigned its own binary variable that is coded 1 if the level applies to the row, and 0 if it does not (see Table 17-1).
TABLE 17-1 Coding a Multilevel Category into a Set of Binary Indicator Variables
StudyID |
PrimaryDx |
HTN |
Diab |
Cancer |
OtherDx |
|---|---|---|---|---|---|
1 |
Hypertension |
1 |
0 |
0 |
0 |
2 |
Diabetes |
0 |
1 |
0 |
0 |
3 |
Cancer |
0 |
0 |
1 |
0 |
4 |
Other |
0 |
0 |
0 |
1 |
5 |
Diabetes |
0 |
1 |
0 |
0 |
Table 17-1 shows theoretical coding for a data set containing the variables StudyID (for participant ID) and PrimaryDx (for participant primary diagnosis). As shown in Table 17-1, you take each level and make an indicator variable for it: Hypertension is HTN, diabetes is Diab, cancer is Cancer, and other is OtherDx. Instead of including the variable PrimaryDx in the model, you’d include the indicator variables for all levels of PrimaryDx except the reference level. So, if the reference level you selected for PrimaryDx was hypertension, you’d include Diab, Cancer, and OtherDx in the regression, but would not include HTN. To contrast this to the education example, in the set of variables in Table 17-1, participants can have a 1 for one or more indicator variables or just be in the reference group. However, with the education example, they can only be coded at one level, or be in the reference group.
Creating scatter charts before you jump into multiple regression analysis
One common mistake researchers make is immediately running a regression or another advanced statistical analysis before thoroughly examining their data. As soon as your data are available in electronic format, you should run error-checks, and generate summaries and histograms for each variable you plan to use in your regression. You need to assess the way the values of the variables are distributed as we describe in Chapter 11. And if you plan to analyze your data using multiple regression, you need special preparation. Namely, you should chart the relationship between each predictor variable and the outcome variable, and also the relationships between the predictor variables themselves.
Imagine that you are interested in whether the outcome of systolic blood pressure (SBP) can be predicted by age, body weight, or both. Table 17-2 shows a small data file with variables that could address this research question that we use throughout the remainder of this chapter. It contains the age, weight, and SBP of 16 study participants from a clinical population.
TABLE 17-2 Sample Age, Weight, and Systolic Blood Pressure Data for a Multiple Regression Analysis
Participant ID |
Age (years) |
Weight (kg) |
SBP (mmHg) |
|---|---|---|---|
1 |
60 |
58 |
117 |
2 |
61 |
90 |
120 |
3 |
74 |
96 |
145 |
4 |
57 |
72 |
129 |
5 |
63 |
62 |
132 |
6 |
68 |
79 |
130 |
7 |
66 |
69 |
110 |
8 |
77 |
96 |
163 |
9 |
63 |
96 |
136 |
10 |
54 |
54 |
115 |
11 |
63 |
67 |
118 |
12 |
76 |
99 |
132 |
13 |
60 |
74 |
111 |
14 |
61 |
73 |
112 |
15 |
65 |
85 |
147 |
16 |
79 |
80 |
138 |
Looking at Table 17-2, let’s assume that your variable names are StudyID for Participant ID, Age for age, Weight for weight, and SBP for SBP. Imagine that you’re planning to run a regression model with this formula (using the shorthand notation described in the earlier section “Defining a few important terms”): SBP ~ Age + Weight. In this case, you should first prepare several scatter charts: one of SBP (outcome) versus Age (predictor), one of SBP versus Weight (another outcome versus predictor), and one of Age versus Weight (both predictors). For regression models involving many predictors, there can be a lot of scatter charts! Fortunately, many statistics programs can automatically prepare a set of small thumbnail scatter charts for all possible pairings among a set of variables, arranged in a matrix as shown in Figure 17-1.

© John Wiley & Sons, Inc.
FIGURE 17-1: A scatter chart matrix for a set of variables prior to multiple regression.
These charts can give you insight into which variables are associated with each other, how strongly they’re associated, and their direction of association. They also show whether your data have outliers. The scatter charts in Figure 17-1 indicate that there are no extreme outliers in the data. Each scatter chart also shows some degree of positive correlation (as described in Chapter 15). In fact, if you refer to Figure 17-1, you may guess that the charts in Figure 17-1 correspond to correlation coefficients between 0.5 and 0.8. In addition to the scatter charts, you can also have your software calculate correlation coefficients (r values) between each pair of variables. For this example, here are the results: 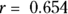 for Age versus Weight,
for Age versus Weight, 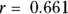 for Age versus SBP, and
for Age versus SBP, and 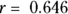 for Weight versus SBP.
for Weight versus SBP.
Taking a few steps with your software
- Assemble your data into a file with one row per participant and one column for each variable you want in the model.
- Tell the software which variable is the outcome and which are the predictors.
- Specify whatever optional output you want from the software, which could include graphs, summaries of the residuals (observed minus predicted outcome values), and other useful results.
Execute the regression (run or submit the code).
Now, you should retrieve the output, and look for the optional output you requested.
Interpreting the Output of a Multiple Regression Analysis
Examining typical multiple regression output
Figure 17-2 shows the output from a multiple regression analysis on the data in Table 17-2, using R statistical software as described in Chapter 4. Other statistical software produces similar output, but the results are arranged and formatted differently.
- Code: The first line starting with Call: reflects back the code run to execute the regression, which contains the linear model using variable names: SBP ~ Age + Weight.

FIGURE 17-2: Output from multiple regression using the data from Table 17-2.
- Residual information: As a reminder, the residuals are the observed outcome values minus predicted values coming from the model. Under Residuals, the minimum, first quartile, median, third quartile and maximum are listed (under the headings Min, IQ, Median, 3Q, and Max, respectively). The maximum and minimum indicate that one observed SBP value was 17.8 mmHg greater than predicted by the model, and one was 15.4 mmHg smaller than predicted.
- Regression or coefficients table: This is presented under Coefficients:, and includes a row for each parameter in the model. It also includes columns for the following:
- Estimate: The estimated value of the parameter, which tells you how much the outcome variable changes when the corresponding variable increases by exactly 1.0 unit, holding all the other variables constant. For example, the model predicts that if all participants have the same weight, every additional year of age is associated with an increase in SBP of 0.84 mmHg.
- Standard error: The standard error (SE) is the precision of the estimate, and is in the column labeled Std. Error. The SE for the Age coefficient is
 mmHg per year, indicating the level of uncertainty around the 0.84 mmHg estimate.
mmHg per year, indicating the level of uncertainty around the 0.84 mmHg estimate. - t value: The t value (which is labeled t value) is the value of the parameter divided by its SE. For Age, the t value is
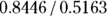 , or 1.636.
, or 1.636. - p value: The p value is designated Pr(>|t|) in this output. The p value indicates whether the parameter is statistically significantly different from zero at your chosen α level (let’s assume 0.05). If
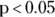 , then the predictor variable is statistically significantly associated with the outcome after controlling for the effects of all the other predictors in the model. In this example, neither the Age coefficient (p = 0.126) nor the Weight coefficient (p = 0.167) is statistically significantly different from zero.
, then the predictor variable is statistically significantly associated with the outcome after controlling for the effects of all the other predictors in the model. In this example, neither the Age coefficient (p = 0.126) nor the Weight coefficient (p = 0.167) is statistically significantly different from zero.
- Model fit statistics: These are calculations that describe how well the model fits your data overall.
- Residual standard error: In this example, the Residual standard error: (bottom of output) indicates that the observed-minus-predicted residuals have a standard deviation of 11.23 mmHg.
- Multiple r2: This refers to the square of an overall correlation coefficient for the multivariate fit of the model, and is listed under Multiple R-squared.
- F statistic: The F statistic and associated p value (on the last line of the output) indicate whether the model predicts the outcome statistically significantly better than a null model. A null model contains only the intercept term and no predictor variables at all. The very low p value (0.0088) indicates that age and weight together predict SBP statistically significantly better than the null model.
Checking out optional output to request
Depending on your software, you may also be able to request several other useful calculations from the regression to be included:
- Predicted values for the dependent variable for each participant. This can be output either as a listing, or as a new variable placed into your data file.
- Residuals (observed minus predicted value) for each participant. Again, this can be output either as a listing, or as a new variable placed into your data file.
Deciding whether your data are suitable for regression analysis
- The amount of variability in the residuals is fairly constant, and not dependent on the value of the dependent variable.
- The residuals are approximately normally distributed.
Figure 17-3 shows two graphs you can optionally request that help you determine or diagnose whether these assumptions are met, so they are called diagnostic graphs (or plots).
- Figure 17-3a provides an indication of variability of the residuals. To interpret this plot, visually evaluate whether the points seem to scatter evenly above and below the line, and whether the amount of scatter seems to be the same across the left, middle, and right parts of the graph. That seems to be the case in this figure.
- Figure 17-3b provides an indication of the normality of the residuals. To interpret this plot, visually evaluate whether the points appear to lie along the dotted line or are noticeably following a curve. In this figure, the points are consistent with a straight line except in the very lower-left part of the graph.
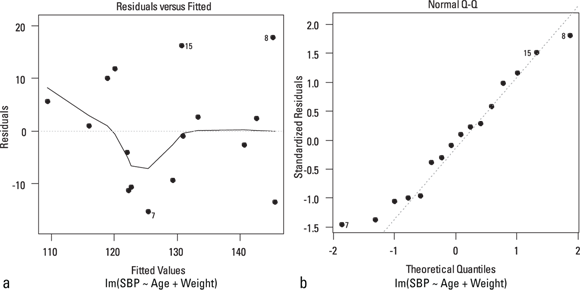
© John Wiley & Sons, Inc.
FIGURE 17-3: Diagnostic graphs from a regression.
Determining how well the model fits the data
Several calculations in standard regression output indicate how closely the model fits your data:
- The residual SE is the average scatter of the observed points from the fitted model. You want them to be close to the line. As shown in Figure 17-2, the residual SE is about
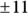 mmHg.
mmHg. - The multiple r2 value represents the amount of variability in the dependent variable explained by the model, so you want it to be high. As shown in Figure 17-2, it is 0.52 in this example, indicating a moderately good fit.
- A statistically significant F statistic indicates that the model predicts the outcome significantly better than the null model. As shown in Figure 17-2, the p value on the F statistic is 0.009, which is statistically significant at α = 0.05.
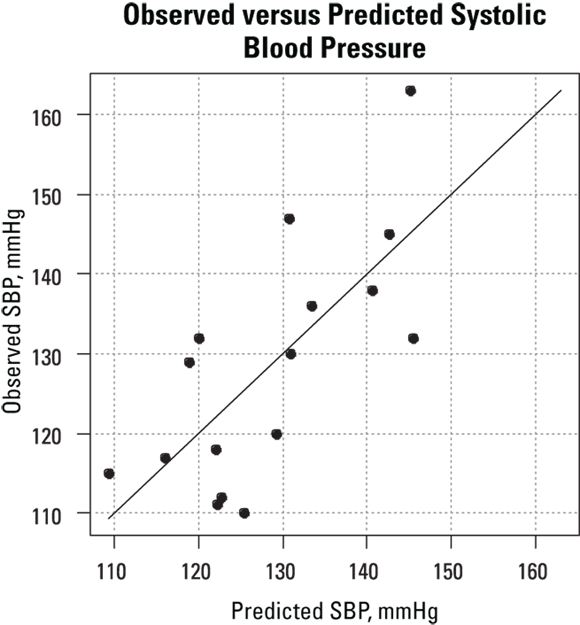
Figure 17-4 shows another way to judge how well the model predicts the outcome. It’s a graph of observed and predicted values of the outcome variable, with a superimposed identity line ( ). Your program may offer this observed versus predicted graph, or you can generate it from the observed and predicted values of the dependent variable. For a perfect prediction model, the points would lie exactly on the identity line. The correlation coefficient of these points is the multiple r value for the regression.
). Your program may offer this observed versus predicted graph, or you can generate it from the observed and predicted values of the dependent variable. For a perfect prediction model, the points would lie exactly on the identity line. The correlation coefficient of these points is the multiple r value for the regression.
© John Wiley & Sons, Inc.
FIGURE 17-4: Observed versus predicted outcomes for the model SBP ~ Age + Weight, for the data in Table 17-2.
Watching Out for Special Situations that Arise in Multiple Regression
Here we describe two topics that come up in multiple regression: interactions (both synergistic and anti-synergistic), and collinearity. Both relate to how the simultaneous behavior of two predictors can influence an outcome.
Synergy and anti-synergy
Sometimes, two predictor variables exert a synergistic effect on an outcome. That is, if both predictors were to be associated with an increase in the outcome by one unit, the outcome would change by more than the sum of the two increases, which is what you’d expect from changing each value individually by one unit. You can test for synergy between two predictors with respect to an outcome by fitting a model that contains an interaction term, which is the product of those two variables. In this equation, we predict SBP using Age and Weight, and include an interaction term for Age and Weight:
SBP = Age + Weight + Age * Weight
If the estimate of the slope for the interaction term has a statistically significant p value, then the null hypothesis of no interaction is rejected, and the two variables are interpreted to have a significant interaction. If the sign on the interaction term is positive, it is a synergistic interaction, and if it is negative, it is called an anti-synergistic or antagonistic interaction.
Collinearity and the mystery of the disappearing significance
When developing multiple regression models, you are usually considering more predictors than just two as we used in our example. You develop iterative models, meaning models with the same outcome variable, but different groups of predictors. You also use some sort of strategy in choosing the order in which you introduce the predictors into the iterative models, which is described in Chapter 20. So imagine that you used our example data set and — in one iteration — ran a model to predict SBP with Age and other predictors in it, and the coefficient for Age was statistically significant. Now, imagine you added Weight to that model, and in the new model, Age was no longer statistically significant! You’ve just been visited by the collinearity fairy.
In the example from Table 17-2, there’s a statistically significant positive correlation between each predictor and the outcome. We figured this out when running the correlations for Figure 17-1, but you could check our work by using the data in Figure 17-2 in a straight-line regression, as described in Chapter 16. In contrast, the multiple regression output in Figure 17-2 shows that neither Age nor Weight are statistically significant in the model, meaning neither has regression coefficients that are statistically significantly different from zero! Why are they associated with the outcome in correlation but not multiple regression analysis?
The answer is collinearity. In the regression world, the term collinearity (also called multicollinearity) refers to a strong correlation between two or more of the predictor variables. If you run a correlation between Age and Weight (the two predictors), you’ll find that they’re statistically significantly correlated with each other. It is this situation that destroys your statistically significant p value seen on some predictors in iterative models when doing multiple regression.
The problem with collinearity is that you cannot tell which of the two predictor variables is actually influencing the outcome more, because they are fighting over explaining the variability in the dependent variable. Although models with collinearity are valid, they are hard to interpret if you are looking for cause-and-effect relationships, meaning you are doing causal inference. Chapter 20 provides philosophical guidance on dealing with collinearity in modeling.
Calculating How Many Participants You Need
Unfortunately, that is not possible in practice, because the equations would be too complicated. Instead, considerations are aimed more toward being able to gather enough data to support a planned regression model. Imagine that you plan to gather data about a categorical variable where you believe only 5 percent of the participants will fall in a particular level. If you are concerned about including that level in your regression analysis, you would want to greatly increase your estimate for target sample size. Although regression models tend to converge in software if they include at least 100 rows, that may not be true depending upon the number and distribution of the values in the predictor variables and the outcome. It is best to use experience from similar studies to help you develop a target sample size and analytic plan for a multiple regression analysis.
 Multiple regression is formally known as the ordinary multiple linear regression model. What a mouthful! Here’s what the terms mean:
Multiple regression is formally known as the ordinary multiple linear regression model. What a mouthful! Here’s what the terms mean:  In textbooks and published articles, you may see regression models written in various ways:
In textbooks and published articles, you may see regression models written in various ways:  Introducing interaction terms into a fitted model and interpreting their significance — both clinically and statistically — must be done contextually. Interaction terms may not be appropriate for certain models, and may be required in others.
Introducing interaction terms into a fitted model and interpreting their significance — both clinically and statistically — must be done contextually. Interaction terms may not be appropriate for certain models, and may be required in others.